Method is Everything in Teaching Math

* Available for seminars / workshops / Pro-D days

As Fall approaches, once again parents and teachers focus on how to achieve educational goals.

"How to" are key words, and that points to method.

It used to be said of teaching Physical Education that all you had to do was "roll out the balls" to get it done. Teaching math with manipulatives needs more than "rolling out the blocks" so to speak. If traditional math teaching was entirely memorizing facts, rules, formulae & process, which mystified math and put success out of reach for most, a better method is essential. Teaching math with manipulatives needs an organized approach, a method that employs principles of child-centred learning based on discovery and understanding.

A method has several elements: key language technique, physical steps, sound principles and a means of assessment. We are people and we are all about the senses & the mind. It precedes the mind in pace of development. Our manual dexterity evolves more quickly than our mentality. Abstract concepts develop only at the onset of puberty (Piaget) Before that, the body rules. All learning must be sensorial to begin with (Montessori).

Explore and Discover,is a major theme in Mortensen Math (MM). Originating in Maria Montessori's approach, MM creates opportunities for the child to explore & discover concepts in math by using hands-on activities to acquire experiences from which to build concepts like addition, subtraction, multiplication and division, factoring and problem solving.

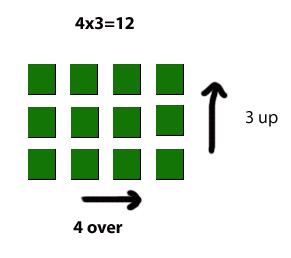
"How to" create learning situations is the challenge facing teachers & parents. merely putting the blocks down in front of the child isn't enough. The manipulatives are attractive, nice to touch, made in pretty colours but more is necessary. A child might wave a crayon around, smell it, eat it, scrawl on a wall, but will need direction if recognizable images are expected. Similarly, playing with the child helps to provoke curiousity and to fire the imagination. If you want rectangles built to facilitate rapid accurate counting, one of the principles of MM, you must first demonstrate building a rectangle.

Play is a bonding experience for children. Showing a child something, then saying, "Show me.." is a great way to become involved for an educator. This is how to share experiences and build relationships with the child. Avoid saying "No" or "No, that's not the way to do it." Instead use phrases like, "That's nice, let's try it this way now" or "can we do it this way too?" The point is ALL experiences are learning experiences. "Getting it wrong" is impossible because mastering the world we live in requires that we discover what doesn't work too. Saying "No" in a directed play situation is counter productive. In addition, using the word "No" sparingly, reserves it's power for dangerous situations when immediate response is vital. Don't waste it on the trivial.

Try this. Good! Now, do it again.

Logically, if you ask a child to do something and he makes an attempt we should encourage them because at least he tried. If he hears "no" a lot, he isn't keen to try next time. Rather we should say, "Good. Now let's do it a different way and see how that works," until we get the desired result. Sure, it takes more patience, but the child is worth it. Encouragement results in children who will be eager to try something, rather than having to be coaxed into it every time. They don't want to hear the word no after making an attempt at it. Nobody likes disapproval. In the long run encouragement works.

For a young child, could having a plastic block named 3 in her hand and counting 4 of them, then counting the unit square markings on the blocks and arriving at 12, be a relevant experience that might lead to understanding?

What use then is memorizing times tables?

MORTENSON MORE THAN MATH employs manipulatives to enhance the child's ability to visualize math concepts, to decode the mathematical language into spatial reality.

The best way I know to explain the Mortensen Math system is to talk about memory first. How good is your short-term memory? More importantly, how good is your short-term memory with numbers? Suppose I gave you 12 numbers, each of them seven digits long. Do you think you could remember them for an hour? Five minutes? Do you think you could remember them long enough to write them down, even right after I told you?

Not likely. That's because you've been taught like everyone else to memorize the hard way. The hard way is how most students are taught math as well.

The truth is the entire math curriculum used in traditional teaching situations, employing textbooks, relies on memorizing nothing but FACTS, RULES, FORMULAE AND PROCESS!

Our job as educators is to decode this mathematical language of symbols into a concrete reality. This is what the method does. More Articles about Teaching Math

Mortensen Math vs. Traditional Teaching

The Difference is Important to Your Child's Success

Parents educated by traditional math teaching, based on memorizing facts, rules, formulae and process, often do not recognize that MM is dramatically different and pass on by, overlooking the tremendous benefits to a method that is based on imagination, visualization and sets nothing less than understanding as its goal.

Our first job as MM educators is to decode this mathematical language into a spatial reality; take for example 4x3=12

All we do in math is count.

See all numbers as rectangles.

Know what one is.

From the above example, picture a rectangle that is four "over" and 3 "up," count the total unit squares.

See 12.

It's that simple.

This: 1, is not one. It is only the name of one written in arabic numerals.

What does one look like?

therefore 4x3=12 looks like this:

more at:

Principles

The additivity of small numbers.

I consider myself liberal-minded when it comes to tolerating the opinions of others. I would rather try gently to persuade them to re-think a problem about which I think they are mistaken than to ban them from expressing their erroneous thinking out loud, after all, I too have been wrong on occasion.

However, I am losing patience with those who claim climate-change theory is a fraud, perpetrated by scientists who have a personal agenda less than scrupulous. In particular I am disturbed by those who deny the notion that human industry has had an impact on climate and will continue to do so. The nay-sayers will nit-pick about any data error and then demand that the entire enterprise be abandoned, presumably because they see nothing amiss in the world that might be prevented from worsening by doing something like say, burning less coal, or turning off unnecessary lighting.

Even those who claim to know some math have said, and are saying, that human activity is not affecting the natural cycle of climate. To them I say, there is something called the law of additivity of small numbers which goes roughly like this: no matter how large a number is, there will always be enough small numbers that, if added together, will exceed it.

What I am driving at is this, maybe one farmer cutting down a forest and planting a single crop for enough years to exhaust the field leaving it unable to absorb C02, or perhaps one coal-fired electricity generator, will not produce orchids in Greenland, but I maintain that if enough of them exist it may happen. By the way, orchids are nice but where does all the ice go?

A mere 7 Billion people burning fossil fuels, destroying forests, creating deserts, clogging rivers and harbours and fish habitat, poisoning lakes with phosphate fertilizer run-off, massacreing sharks for their fins, slaughtering lions and rhinos for aphrodisiacs, etc. may not destroy the planet today. But by 2050 there will be 9 Billion. By 3000 who knows. If you think 7 billion won't kill the planet or alter the climate, you surely must concede that there is SOME number of people who could. It took a huge number of Chinese with buckets to move a mountain to build the 3 Rivers dam, but they did it.

There used to be forests in Sudan, now there is only desert. When only a few bedouin took trees for firewood the sands were held at bay, but when millions burnt wood for cooking, and heat the desert took over. Man destroyed the local climate and he didn't need bulldozers and dynamite. They did it with their bare hands, one twig at a time. Just like the Chinese built the dam.

Kill one coyote, no problem; kill enough of them and the jackrabbits will eat the entire grazing lands leaving no food for cattle. One grasshopper, no problem; a million locusts and you have famine, it's about the additivity of small numbers.

R.I.P. Needy Cat It had rained during the night. I had awakened several times disturbed by the memories of images from yesterday and I heard the downpour. It roared on the roof of the house and water cascaded from the gazebo in the backyard. I stood at the backdoor staring out at the rain through the screen door and my heart was broken. The willow dripped. It was weeping too. Yesterday morning, the twelfth of June, was bright and sunny. The first day of summer was nigh. I had walked to the car and glanced to the end of the driveway where I saw our tuxedo cat lying on the hot pavement like an old hound dog. Her back was towards me and her legs stretched out as if she had just rolled over to scratch her back and was resting. It was quiet on the street where children often rode their bikes laughing and ringing bells and mothers chatted pushing strollers as they exercised. Then a magpie landed just a few feet from her with a flap of the wings and a squawk. That was when I knew something was wrong. The sun glistened on the bird's black shiny feathers, its white shoulders were bright in the sunshine. It looked at me and took a tentative step towards the resting cat, but the cat did not move. I hurried to her, shooing the bird away. It would not have been so brave if things were right and normal in the world. She had appeared wide eyed and desperate in our garden eighteen months ago, looking lean and frightened. Her expression prompted Eileen to name her Needy Cat. She was black with a white chest and belly and four white feet, a spiffy tuxedo cat. Her tail was long and expressive, a lovely animal. No collar, no tattoo that I could see. She was about a year old and let me pick her up without complaining. When she hadn't gone away after a day or two I put down a dish for her. We had had a beloved outside cat who had died a year before Needy came to us, a ginger named Bailey. I put kibble out on the stoop where previously I had placed food for Bailey. Sometimes life seems so circular. There was a large metal bowl under the outside tap at the rear of the house to catch drips. Sometimes it harboured a frog. Needy Cat found a safe place to sleep among some boxes in the carport and before long I had put out a basket for her with an old blanket. The nights grew shorter and though we didn't let her inside - we had an older, inside cat named Ellie, she hadn't left. Then I put her basket into a large cardboard box on top of the others where she could have a good view of things, maintaining the high ground, and I draped a blanket partly over the front to keep out the draft. When the snows came I put a small lamp with a 25 watt bulb into the box. She had passed two winters that way and on a summer's day she would rest in my lap purring Now, she was gone. I knelt beside her on the edge of the roadway. She hadn't even managed to make it to the safety of the driveway after being struck, so it must have been instantaneous. She was still warm and soft when I got to her. I had still hoped she would get up when I stroked her, and follow me into the house, but her eyes were lifeless and she was not breathing. I picked her up and carried her to the carport. The magpie lurked. I told Eileen that Needy Cat had been hit by a car and had died. She was horrified. "No! It can't be,” she protested. “I was just petting her ten minutes ago!" I put my arms around her, and we consoled each other. I had played with Needy myself half an hour before as I did every morning when I put out her kitty kibble. She showed me the bright wide-eyed look that had earned her her name, then she was face down in her breakfast. The suddenness of it was what shocked me. One minute a loved pet, part of the household plans when booking a trip, an undeniable element of our daily lives, was there, a complex life with moods and attitudes, an object of adoration, then, abruptly, she was absent without warning, never to return. We held each other, knowing in some part of our hearts, that we were just as vulnerable. I tried to sleep last night but the images of her, lying in the road as the magpie arrived remorselessly, dispassionately, to peck at her, her limp body slumped in my hands, the trickle of blood falling from her mouth, disturbed my dreams. The rain I saw at 5am, bouncing off the metal roof of the shed in the gray of pre-dawn, completed my misery. I wanted to tell someone what a rotten cat she had been, all the nuisance she had caused, about the scratches, the expense, the trouble I had gone to, in making a bed for her, heat lamp and all, to make me miss her less. I started writing it down, and here at the keyboard, was where Eileen found me this morning, tears dripping onto my fingers.

Long Distance and the Meaning of Life

I have just finished reading Bill McKibben's book, "Long Distance" the story of a year in his life training to be the best skinny-skier he could be, with a coach and everything, during which his father came to the end of his life. The latter was unplanned, and unexpected as his siblings and father had lived to their nineties but he had succumbed to brain cancer at 68.

In the book Bill seeks the meaning of life among other things - like the right wax for his skis at zero degrees Celsius. He ends with completing the metaphor of life as an endurance race. Much of what he wrote stimulated my thoughts and I want to explore them in writing.

The meaning of life is the substance of every book I've ever read implicitly, if not explicitly. Just as life's experience is the mother of metaphor, It is also the fodder of all writing, pun intended.

The daily routine is the core of identity, not singular achievements or unique experiences. Identity is founded in the quotidian, not the rare. Mantras, endlessly repeated, rituals performed until they are rote and literally taken for granted - exactly as they are intended to be, things done without thinking, more define the individual than stunning achievements, like finishing an Ironman, say, or writing a novel, or winning an award, say who we are. One can wear the t-shirt proclaiming the achievement but as days pass it loses its lustre and fades as does the memory of the achievement. It is merely what we once did not who we are, despite Mike or Steve's voice ringing in our ears, Daily workouts, oft=repeated doses of kilometres run, or biked, the constant association of ourselves with the omnipresent bag of workout gear, the bike on the rack behind the car, declare our identity, state unambiguously who we are. As Sartre said, it is what we do that makes us who we are.

Scotia Bank wants dumb customers,

.. they are more profitable.
March 1st Scotiabank puts up chequing account and other fees. The simplest account – a personal chequing account, used by millions of Canadians, goes up to $5.95 from $3.95. Two bucks. That’s 33% increase in fees on your personal chequing account.
Suppose Scotiabnk has 10 million customers across Canada. They ask for $2 more from each person and they get $20 million per month, or $240,000,000 per year – a quarter of a Billion dollars just added to their bottom line. They didn’t have to do a thing to earn it. They aren’t giving any new services for that. They just asked every personal account customer for another $2. It’s that simple.

Now, you can imagine some people may move their accounts to another institution, one that offers no-fee chequing say. Those will be the smart people, who read the notice included in their statement, who realize they just got dinged another $24 per year for nothing. Does the bank care? No. Those smart people were probably their most troublesome customers anyway. If they were also valuable customers, with large debts (interest paying, say) then the bank would probably waive their personal chequing account fees if they asked. If they weren’t profitable customers, then good riddance to them. This is called culling the herd. Raise the fees, get rid of the smart, troublesome customers. Keep the dumb profitable ones.

Scotiabank wants dumb, profitable customers. They want people who don’t make demands, ask awkward questions, like “Why should I pay an additional $24 per year for my personal chequing account anyway? I put my paycheques into it, you don’t give me any interest on that money, yet you get to use it to loan to other people and earn interest, but I don’t get any of that. I just pay fees. Why is that anyway?”

“Good-bye, nice knowing you,” is the bank’s unspoken response. “See ya, wouldn’t want to be ya.”

Also, the fee for using your debit card more than the allowed number of times each month goes up from $0.65 to $1 – that’s right 35%. Of course, you don’t get any additional services for that; it is just profit added to the bank’s bottom line. Thanks, sucker.

Insidiously, Scotiabank has waived debit fees for students under 19 years of age. Why is that I wonder? Could it be to train the youngsters into exclusive use of their debit cards so that when they hit adulthood, they will choose a monthly fee plan instead of cutting back on the use of the debit card?

You see banks don’t want us to use cash. They charge current account holders for depositing cash. That’s right. If you are a business, say, a clothing store, or a photocopy shop, Scotiabank charges you a fee for depositing cash. They say it costs them to ship all that paper to the central clearing house. How troublesome it must be for them. They actually have to count the money people give them for safekeeping. It’s much cheaper to let the computer count the transactions. Better yet, if we can train people when they are young to use a debit card for everything, then when they grow up they won’t want cash anyway, spoils the line of your jeans you know. Then we can ding them a monthly fee to use that debit card and raise it every once in a while. In time we can bleed them dry and they won’t even notice. Remember that story about the frog in the pot of boiling water?