Science, not Superstition

Harrison Ford made an impassioned plea in a speech recently, that we should stop electing people to power who do not believe in science.

https://www.youtube.com/watch?v=v4sA_EwNPmY

I sympathize with Ford's frustration. Part of the challenge we face, we scientists, is the language we have to use to discuss the problem. Ford asks us not to give power to those who don't "believe" in science, but science is the antithesis of "belief."

The value of science is that it works whether you believe in it or not. That's because it is a method rather than received wisdom as religions are. The law of gravity or the theory of evolution are not received wisdom handed down by elders, they are simply observations of how things around us seem to work. I have never seen a dropped pencil not fall to the floor. I see a food source, say nuts, cease to grow on an island (think Galapagos) and the critters who ate them die out and I think, "that's how it goes."

It's not about believing in science, it's about having a method of understanding the world around us that is based on evidence not superstition. Ford should rather have said, stop electing people who "believe" in superstition, eg. Reagan and his astrology, or wishful thinking, eg. Trump's meteorological scheme, or the preaching's of scam artists, eg. Mormon Mitt Romney who believes the Book of Mormon presumably, else he's also a hypocrite.

Bertrand Russell, (1872-1970) Professor of philosophy, Cambridge U. wrote, "we ought not to believe in that for which there is no evidence.".

Night Ride Backwards in Time

Fifty years ago tonight I was riding my bicycle through the darkened streets of Bournemouth from my boarding school proper, to the dormitory where I slept. It was damp as it always was in January in coastal towns in England. I sometimes detoured down Durley Chine and over to Alum Chine to delay arriving at the dorm where only bedtime awaited me, and to experience the rush of careening through the shadows between street lights exhilarated by the speed and the fear of crashing into someone walking his dog or slipping on damp leaves and falling into the chasm that ran down the centre of what was really a drainage ditch down which storm waters raged occasionally to the sea. It was the cold, damp sea air blowing up those darkened pathways that came rushing back to me. Those were vivid memories, brought back suddenly to me tonight at 63 years of age halfway around the world from England, yet it seemed like I had been transported across time and space to that earlier time in another place.

It was damp this evening in Longtan Township, Taiwan, forty kilometres south of Taipei, 74% humidity in fact, according to the weathernetwork.com. I was riding my bicycle through the darkened streets, keeping a lookout for stray dogs that lurked along this road just as I had as a schoolboy long ago in England. I felt the chill from the damp air as I passed the itinerant gardens of locals that filled the green spaces between blocks of apartments spaced at half kilometre intervals along Meilong Road, on the way to my residence. I lived in teacher’s rooms at the dormitory of one of Taiwan’s best boarding schools, where I was a schoolmaster. The eerie similarity struck me with some force as I unzipped my jacket and felt the cool, moist air hit my chest and neck. Was I stuck in some half century long rut of life in a boarding school environment, forever living in rooms, eating at the cafeteria, as if never growing up or adopting a regular life like other folks?

The resemblances were striking, it was not just a metaphor, the bike riding – I have been doing that all my life, then as a commuting vehicle to school, now because triathlon is my hobby, my passion, the dormitory then because I was a boarder, now because I am here alone and the dorm room is free, which saves a lot of money, when you add in meals, the damp air, the night ride, it was uncanny how history, my story, repeats itself.

Then, I was learning, never suspecting I might become a schoolteacher myself. Now, I was enjoying the interaction with the students, a great bunch of kids 15 to 17 years of age from well-off families in Taiwan, feeling that maybe I was making a positive contribution to their lives. I certainly never hoped that any of them would end up as a teacher, perhaps living in a boarding school in England. That would be too ironic.

Why do some kids hate math? Just as a thought experiment, if I surveyed all secondary school students, asking them what subject they would most like to cut if given a free pass, what would it be? I am guessing the majority would choose Math. I wonder, does this concern all secondary math teachers? I don't mean to dump on these fine professionals. They love kids, love teaching and are highly skilled at what they do. But the fact remains. What can be done? The fact that most kids find math to be an unattractive subject suggests to me that the environment is at fault. Jerry Mortensen used to make the point that kids learn a foreign language by the age of three without the aid of a university-trained tutor or any formal instruction, why? because they lived in a language-rich environment - adults talking, TV, songs with lyrics, Alphagetti. Can we create a math-rich environment? What would that look like? Posters on the walls of Einstein, Archimedes, Pythagoras, Emma Noether, Ramanujan perhaps. Mobiles of geodesics & other polyhedrons, colourful manipulatives available to play with & build stuff. Math cookies? Skip-counting songs - rap, lullabies, fugues - if you use 'em as teaching tools? People learn using all their senses. What environment would a truly great math teacher create for her students? What would you say if the kids told you they didn't want to go out for recess, they wanted to stay in and play some more math? It happens, guess where. More at: http://www.geoffwhite.ws/math-rich.html

Memorization Cannot Lead to Understanding

Memorization and Understanding in Mathematics

by Geoff White, B.Ed. (Southampton, UK)

* Available for seminars / workshops / Pro-D days

In this article I argue that mere memorization of symbols cannot logically lead to understanding, with reference to the thought experiment: John Searle's Chinese room

To begin, here is a synopsis of the Chinese Room argument by John Searle:

from Wikipedia article:

"The Chinese room is a thought experiment by John Searle which first appeared in his paper "Minds, Brains, and Programs", published in Behavioral and Brain Sciences in 1980.[1] It addresses the question: if a machine can convincingly simulate an intelligent conversation, does it necessarily understand? In the experiment, Searle imagines himself in a room acting as a computer by manually executing a program that convincingly simulates the behavior of a native Chinese speaker. People outside the room slide Chinese characters under the door and Searle, to whom "Chinese writing is just so many meaningless squiggles",[1] is able to create sensible replies, in Chinese, by following the instructions of the program; that is, by moving papers around. The question arises whether Searle can be said to understand Chinese..?" ..Searle's Chinese Room Argument which holds that a program cannot give a computer a "mind" or "understanding", regardless of how intelligently it may make it behave.

He concludes that "I can have any formal program you like, ..but I still understand nothing."

The Chinese room is ..Searle's argument .. directed against functionalism and computationalism (philosophical positions inspired by AI), rather than the goals of applied AI research itself. [5] The argument leaves aside the question of creating an artificial mind by methods other than symbol manipulation."

Let's take Searle's thought experiment a bit further to see what it may tell us about children learning mathematics.

Suppose a dedicated human subject commits to translating Chinese into Russian in Cyrillic characters under the same conditions as John Searle in the above - she is a native speaker of English and knows nothing of either language She is given charts and manuals to assist her in producing the appropriate Russian response to given Chinese pictograms which she receives through a slot in the door. There are no pictures to aid her. She consults only with her books and charts and writes out the response on paper then slides it back out through the door. After a while she gets pretty good at this and has memorized certain combinations of Russian characters in response to Chinese pictograms that she has seen before. Later she is able to "translate" the Chinese symbols into Russian ones with only an occasional consultation with her Chinese - Russian dictionary and the grammar charts.

Can we say that she understands either language?

She still does not know what the Chinese pictograms mean in English, nor does she know the English equivalent of any Russian word. We might even provide her with tapes of how to pronounce each Chinese Pictogram and she can read the Chinese messages aloud so that a Chinese speaker could know what she is reading. Can she speak Chinese?

Let's say she has been translating a cookbook, remember no pictures, no smells or tastes either. Some of the recipes are among her favorite dishes but she has no way of knowing that. Would her mouth water in reading about them in Chinese the way it might if she read an English cookbook?

Serious contemplation of the experiment reveals that what is missing, what is so vital to our understanding of a language, even our own, is the relevant tactile motor kinaesthetic and other sensory experiences associated with each word or concept that denotes them. From birth we learn language cues in concert with the sight, feel, taste, smell or sound of an experience when the word is presented to us. The special case of Helen Keller is a vivid demonstration of how difficult learning language is without seeing, or hearing. Touch was the only major avenue for her to acquire language. Could she have achieved language at all if she also lacked hands? I argue, as does John Searle above, that meaning and understanding and the development of concepts are only possible with the relevant sensory experiences.

Given a string of symbols then, say "abhor," a child could not possibly impute any meaning to it, thus understanding is impossible merely by repetition, by memorization. Consider the jabberwocky poem. You can memorize it but it is still meaningless. Let's go a step further.

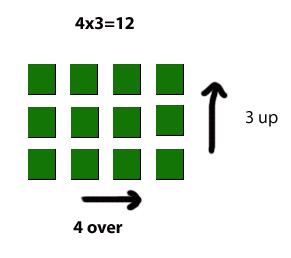
Given these symbols: x²±5=14 a child could not tell if it was truthful or meaningless. By extension, memorizing 4x3=12 until the response "12" can be given to the prompt "4x3?" cannot be said to demonstrate understanding of multiplication, nor of 12 or 4 or 3 or anything at all.

Logically then, without the relevant sensory experiences, a child cannot come to understand multiplication or numbers merely by memorizing times tables.

What might the relevant experiences be?

For a young child, could having a plastic block named 3 in her hand and counting 4 of them, then counting the unit square markings on the blocks and arriving at 12, be a relevant experience that might lead to understanding?

What use then is memorizing times tables?

MORTENSON MORE THAN MATH employs manipulatives to enhance the child's ability to visualize math concepts, to decode the mathematical language into spatial reality.

The best way I know to explain the Mortensen Math system is to talk about memory first. How good is your short-term memory? More importantly, how good is your short-term memory with numbers? Suppose I gave you 12 numbers, each of them seven digits long. Do you think you could remember them for an hour? Five minutes? Do you think you could remember them long enough to write them down, even right after I told you?

Not likely. That's because you've been taught like everyone else to memorize the hard way. The hard way is how most students are taught math as well.

The truth is, the entire math curriculum used in traditional teaching situations, employing textbooks, relies on memorizing nothing but FACTS, RULES, FORMULAE AND PROCESS!

Our job as educators is to decode this mathematical language of symbols into a concrete reality. This is what the method does.

see more at:

www.geoffwhite.ws

Method is Everything in Teaching Math

* Available for seminars / workshops / Pro-D days

As Fall approaches, once again parents and teachers focus on how to achieve educational goals.

"How to" are key words, and that points to method.

It used to be said of teaching Physical Education that all you had to do was "roll out the balls" to get it done. Teaching math with manipulatives needs more than "rolling out the blocks" so to speak. If traditional math teaching was entirely memorizing facts, rules, formulae & process, which mystified math and put success out of reach for most, a better method is essential. Teaching math with manipulatives needs an organized approach, a method that employs principles of child-centred learning based on discovery and understanding.

A method has several elements: key language technique, physical steps, sound principles and a means of assessment. We are people and we are all about the senses & the mind. It precedes the mind in pace of development. Our manual dexterity evolves more quickly than our mentality. Abstract concepts develop only at the onset of puberty (Piaget) Before that, the body rules. All learning must be sensorial to begin with (Montessori).

Explore and Discover,is a major theme in Mortensen Math (MM). Originating in Maria Montessori's approach, MM creates opportunities for the child to explore & discover concepts in math by using hands-on activities to acquire experiences from which to build concepts like addition, subtraction, multiplication and division, factoring and problem solving.

"How to" create learning situations is the challenge facing teachers & parents. merely putting the blocks down in front of the child isn't enough. The manipulatives are attractive, nice to touch, made in pretty colours but more is necessary. A child might wave a crayon around, smell it, eat it, scrawl on a wall, but will need direction if recognizable images are expected. Similarly, playing with the child helps to provoke curiousity and to fire the imagination. If you want rectangles built to facilitate rapid accurate counting, one of the principles of MM, you must first demonstrate building a rectangle.

Play is a bonding experience for children. Showing a child something, then saying, "Show me.." is a great way to become involved for an educator. This is how to share experiences and build relationships with the child. Avoid saying "No" or "No, that's not the way to do it." Instead use phrases like, "That's nice, let's try it this way now" or "can we do it this way too?" The point is ALL experiences are learning experiences. "Getting it wrong" is impossible because mastering the world we live in requires that we discover what doesn't work too. Saying "No" in a directed play situation is counter productive. In addition, using the word "No" sparingly, reserves it's power for dangerous situations when immediate response is vital. Don't waste it on the trivial.

Try this. Good! Now, do it again.

Logically, if you ask a child to do something and he makes an attempt we should encourage them because at least he tried. If he hears "no" a lot, he isn't keen to try next time. Rather we should say, "Good. Now let's do it a different way and see how that works," until we get the desired result. Sure, it takes more patience, but the child is worth it. Encouragement results in children who will be eager to try something, rather than having to be coaxed into it every time. They don't want to hear the word no after making an attempt at it. Nobody likes disapproval. In the long run encouragement works.

For a young child, could having a plastic block named 3 in her hand and counting 4 of them, then counting the unit square markings on the blocks and arriving at 12, be a relevant experience that might lead to understanding?

What use then is memorizing times tables?

MORTENSON MORE THAN MATH employs manipulatives to enhance the child's ability to visualize math concepts, to decode the mathematical language into spatial reality.

The best way I know to explain the Mortensen Math system is to talk about memory first. How good is your short-term memory? More importantly, how good is your short-term memory with numbers? Suppose I gave you 12 numbers, each of them seven digits long. Do you think you could remember them for an hour? Five minutes? Do you think you could remember them long enough to write them down, even right after I told you?

Not likely. That's because you've been taught like everyone else to memorize the hard way. The hard way is how most students are taught math as well.

The truth is the entire math curriculum used in traditional teaching situations, employing textbooks, relies on memorizing nothing but FACTS, RULES, FORMULAE AND PROCESS!

Our job as educators is to decode this mathematical language of symbols into a concrete reality. This is what the method does. More Articles about Teaching Math

Mortensen Math vs. Traditional Teaching

The Difference is Important to Your Child's Success

Parents educated by traditional math teaching, based on memorizing facts, rules, formulae and process, often do not recognize that MM is dramatically different and pass on by, overlooking the tremendous benefits to a method that is based on imagination, visualization and sets nothing less than understanding as its goal.

Our first job as MM educators is to decode this mathematical language into a spatial reality; take for example 4x3=12

All we do in math is count.

See all numbers as rectangles.

Know what one is.

From the above example, picture a rectangle that is four "over" and 3 "up," count the total unit squares.

See 12.

It's that simple.

This: 1, is not one. It is only the name of one written in arabic numerals.

What does one look like?

therefore 4x3=12 looks like this:

more at:

Principles

The additivity of small numbers.

I consider myself liberal-minded when it comes to tolerating the opinions of others. I would rather try gently to persuade them to re-think a problem about which I think they are mistaken than to ban them from expressing their erroneous thinking out loud, after all, I too have been wrong on occasion.

However, I am losing patience with those who claim climate-change theory is a fraud, perpetrated by scientists who have a personal agenda less than scrupulous. In particular I am disturbed by those who deny the notion that human industry has had an impact on climate and will continue to do so. The nay-sayers will nit-pick about any data error and then demand that the entire enterprise be abandoned, presumably because they see nothing amiss in the world that might be prevented from worsening by doing something like say, burning less coal, or turning off unnecessary lighting.

Even those who claim to know some math have said, and are saying, that human activity is not affecting the natural cycle of climate. To them I say, there is something called the law of additivity of small numbers which goes roughly like this: no matter how large a number is, there will always be enough small numbers that, if added together, will exceed it.

What I am driving at is this, maybe one farmer cutting down a forest and planting a single crop for enough years to exhaust the field leaving it unable to absorb C02, or perhaps one coal-fired electricity generator, will not produce orchids in Greenland, but I maintain that if enough of them exist it may happen. By the way, orchids are nice but where does all the ice go?

A mere 7 Billion people burning fossil fuels, destroying forests, creating deserts, clogging rivers and harbours and fish habitat, poisoning lakes with phosphate fertilizer run-off, massacreing sharks for their fins, slaughtering lions and rhinos for aphrodisiacs, etc. may not destroy the planet today. But by 2050 there will be 9 Billion. By 3000 who knows. If you think 7 billion won't kill the planet or alter the climate, you surely must concede that there is SOME number of people who could. It took a huge number of Chinese with buckets to move a mountain to build the 3 Rivers dam, but they did it.

There used to be forests in Sudan, now there is only desert. When only a few bedouin took trees for firewood the sands were held at bay, but when millions burnt wood for cooking, and heat the desert took over. Man destroyed the local climate and he didn't need bulldozers and dynamite. They did it with their bare hands, one twig at a time. Just like the Chinese built the dam.

Kill one coyote, no problem; kill enough of them and the jackrabbits will eat the entire grazing lands leaving no food for cattle. One grasshopper, no problem; a million locusts and you have famine, it's about the additivity of small numbers.